圖形推理中折疊問題-2019年公務(wù)員聯(lián)考行測解題技巧

　　行測圖形推理就是考查你的空間思維，很多小伙伴們在筆試時都是借助橡皮擦這個特殊的工具解題，但萬一被監(jiān)考老師抓住視為作弊就得不償失了。為此本文小編詳細介紹圖形推理題的解題原理，讓你徹底掌握折疊圖形題型的破解之法。

　　解題思路：通過平面圖形的性質(zhì)來分析立體圖形空間特征。圖形折疊后的性質(zhì)很多是可以從平面圖形中直接反映出來的，比如哪些面必然是對立的，哪些面必然是相鄰的，每個面上直線的方向等。

　　解題方法：排除法。利用平面圖形的性質(zhì)可以快速排除錯誤選項，有利于快速解題。

　　正方體（六面體）表面展開圖的性質(zhì)

　　你知道正方體表面展開圖有多少種嗎？解答：11種

　　圖中“上”和“下”，“左”和“右”，“前”和“后”互為對立面。說明：下面的“一四一”型、“二三一”型指展開圖形每一列有幾個圖形。

　　1．“一四一”型

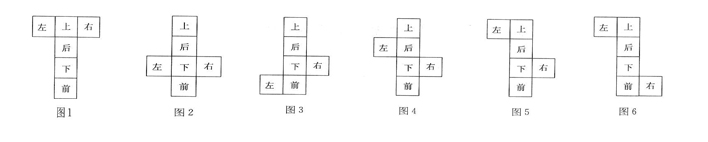
　　2．“二三一”型

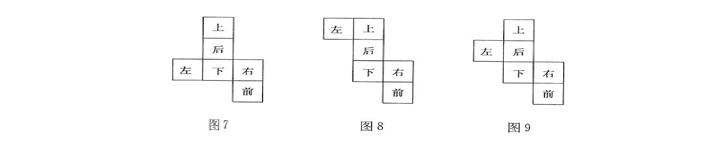
　　3．“三三”型和“二二二”型

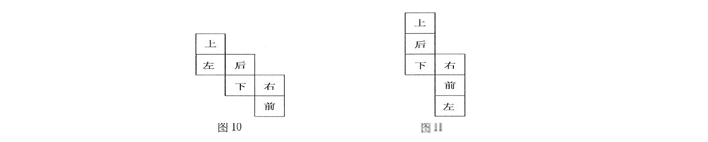
　　下面來幾組真題檢測一下 ↓ ↓ ↓

　　【例題1】

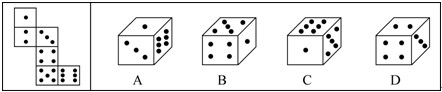
　　左邊給定的是紙盒的外表面，下面哪一項能由它所折疊而成（  ）

　　解析：由以上性質(zhì)可以可以看出，一點面和四點面為對立面，B項錯誤；C項中一點面與六點面構(gòu)成如圖相鄰關(guān)系時，五點面應(yīng)位于左面而右頂面（可以六點面為上面折疊），排除；二點面、三點面、四點面三面相鄰，且公共頂點不變，三點面方向不對，D項錯誤。

　　注：平面圖形的公共頂點和公共邊折疊成多面體后仍為這三個面的公共頂點和公共邊。（通過上圖D項可驗證）

　　【例題2】

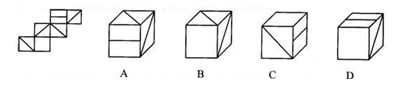
　　左邊給定的是紙盒的外表面，下面哪一項能由它所折疊而成（  ）

　　解析：橫線面和空白面為對立面，C、D項錯誤；A項中右表面的對角線應(yīng)該與上表面的對角線相交在一個頂點上，排除。

　　【例題3】

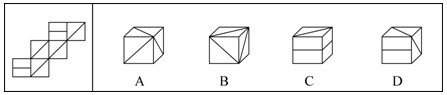
　　左邊給定的是紙盒的外表面，下面哪一項能由它折疊而成？

　　解析：A項三條斜線不可能交于一點，排除。C項兩條水平線不會交于一點，排除。D項正面應(yīng)為豎直線，排除。

　　【例題4】

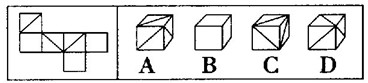
　　解析：B。

　　解法一：三個空白面都不相互對立，是相鄰的，B項正確。

　　解法二：三條對角線不會交于一點，也不會首尾相連，排除C、D兩項；前表面和右表面的線段交點應(yīng)該是在下方，排除A項，所以B項正確。

　　以上就是這篇的全部內(nèi)容，想要刷題？這里有最新版【實戰(zhàn)題庫5600題】，全套10本，每一個知識點都能夠被反復(fù)練習。