數量
均值不等式求極值-2025國家公務員考試行測解題技巧
http://www.ssrtes.com 2024-09-04 09:40 來源:永岸公考
極值問題是行測數量關系中較為常見的一類問題,其中均值不等式求極值,大家在學生時代接觸過,但現在可能感覺既陌生又熟悉,印象已經并不深刻了。今天整理了有關均值不等式求極值的知識點,為大家答疑解惑。
一、概念
若a,b是實數,則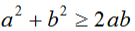 ,等號當且僅當a=b的時候取得。
,等號當且僅當a=b的時候取得。
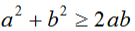 ,等號當且僅當a=b的時候取得。
,等號當且僅當a=b的時候取得。 二、推論
和定差小積最大,當正實數a、b的和為定值時,當且僅當a=b,a與b的乘積可取到最大值。
三、應用
【例1】某商品的進貨單價為80元,銷售單價為100元,每天可售出120件。已知銷售單價每降低1元,每天可多售出20件。若要實現該商品的銷售利潤最大化,則銷售單價應降低的金額是:
A.5元
B.6元
C.7元
D.8元
答案:C
【解析】設應降低x元,總利潤為y元,則降低后的銷售單價為(100-x)元,銷量為(120+20x)件,進貨單價為80元,則總利潤y=(100-x-80)×(120+20x),將其化簡成函數式為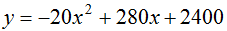 ,根據一元二次函數圖像性質,當
,根據一元二次函數圖像性質,當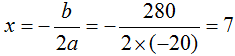 時,y最大。故本題選C。
時,y最大。故本題選C。
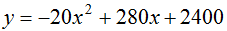 ,根據一元二次函數圖像性質,當
,根據一元二次函數圖像性質,當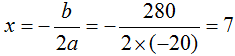 時,y最大。故本題選C。
時,y最大。故本題選C。 【例2】某類商品按質量分為8個檔次,最低檔次商品每件可獲利8元,每提高一個檔次,則每件商品的利潤增加2元。最低檔次商品每天可產出60件,每提高一個檔次,則日減少5件。若只生產其中某一檔次的商品,則每天能獲得的最大利潤是( )元。
A.620
B.630
C.640
D.650
答案:C
【解析】設提高x檔,則每件產品的利潤增加2x元,日產量減少5x件,總利潤為y元,每天獲得的利潤為y=(8+2x)×(60-5x)=10×(4+x)×(12-x)元,因為(4+x)+(12-x)=16是定值,根據均值不等式原理,故當且僅當4+x=12-x時,即x=4時,(4+x)×(12-x)的值最大,即可獲得最大利潤,為10×(4+4)×(12-4)=640元。故本題選C。
免費學習資源(關注可獲取最新開課信息)


















